The COVID-19 Modelling (CoMo) Consortium Model
Age-structured epidemiological model with health care utilization
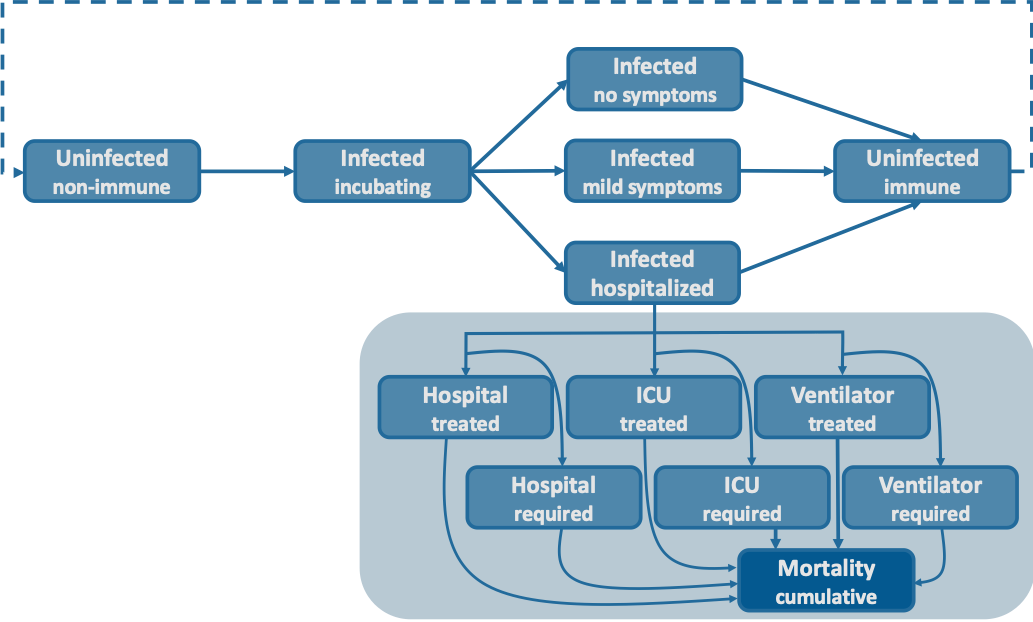 Image credit: CoMo Consortium
Image credit: CoMo Consortium
The age structured SEIR model with infected compartments stratified by symptoms, severity and treatment seeking and access.
The model uses publicly available country-specific data to define the population structure 1 as a model input. The model interface uses publicly available country-specific data on cases and mortality 2 for visual calibration of model parameters to user selected baseline scenarios. More elaborate calibration methods are under consideration but are not a priority since the system is unidentifiable and therefore calibration will be entirely dependent on user-selected baseline scenarios.
The model interface can be found here: https://comomodel.net/. The equations for the basic model structure follow (Equation 1).
\[ \begin{aligned} \frac{dS}{dt} ~ & = ~ -S ~ \circ ~ \Lambda ~ + ~ \omega R ~ + ~ A ~ \cdot ~ S ~ - ~ \mu ~ \cdot ~ S ~ + ~ bP \\ \\ \frac{dE}{dt} ~ & = ~ S ~ \circ ~ \Lambda ~ - ~ \gamma E ~ + ~ A ~ \cdot ~ E ~ - ~ \mu ~ \cdot ~ E \\ \\ \frac{dI}{dt} ~ & = ~ \gamma(1 ~ - ~ p_{clin})(1 ~ - ~ p_{ihr}) ~ \cdot ~ E ~ - ~ v_I I ~ + ~ A ~ \cdot ~ I ~ - ~ \mu ~ \cdot ~ I \\ \\ \frac{dC}{dt} ~ & = ~ \gamma p_{clin}(1 ~ - ~ p_{ihr}) ~ \cdot ~ E ~ - ~ v_I C ~ + ~ A ~ \cdot ~ C ~ - ~ \mu \cdot C \\ \\ \frac{dR}{dt} ~ & = ~ v_I (I ~ + ~ C) ~ + ~ A ~ \cdot ~ R ~ - ~ \omega R ~ - ~ \mu ~ \cdot ~ R ~ + ~ (1 ~ - ~ \delta_H p_{ifr})v_H ~ \cdot ~ H \\ ~ & + ~ (1 ~ - ~ \delta_{H_c} p_{ifr})v_H ~ \cdot ~ H ~ + ~ (1 ~ - ~ \delta_U p_{ifr})v_U ~ \cdot ~ U \\ ~ & + ~ (1 ~ - ~ \delta_{U_c} p_{ifr})v_U ~ \cdot ~ U ~ + ~ (1 ~ - ~ \delta_{V} p_{ifr})v_V ~ \cdot ~ V \\ ~ & + ~ (1 ~ - ~ \delta_{V_c} p_{ifr})v_V ~ \cdot ~ V \\ \\ \frac{dH}{dt} ~ & = ~ p_{ihr}(1 ~ - ~ p_U)(1 ~ - ~ p{K_H})\gamma E ~ - ~ v_H H ~ + ~ A ~ \cdot ~ H ~ - ~ \mu ~ \cdot ~ H \\ \\ \frac{dH_c}{dt} ~ & = ~ p_{ihr}(1 ~ - ~ p_U)p_{K_H}\gamma E ~ - ~ v_H H_c ~ + ~ A ~ \cdot ~ H_c ~ - ~ \mu ~ \cdot ~ H_c \\ \\ \frac{dU}{dt} ~ & = ~ p_{ihr} p_U (1 ~ - ~ p_{K_U})(1 ~ - ~ p_V)\gamma E ~ - ~ v_U U ~ + ~ A ~ \cdot ~ U ~ - ~ \mu ~ \cdot ~ U \\ \\ \frac{dU_c}{dt} ~ & = ~ p_{ihr} p_U p_{K_U} (1 ~ - ~ p_v)\gamma E ~ - ~ v_U U_c ~ + ~ A ~ \cdot ~ U_c ~ - ~ \mu ~ \cdot ~ U_c \\ \\ \frac{dV}{dt} ~ & = ~ p_{ihr} p_U(1 ~ - ~ p_{K_U})(1 ~ - ~ p_{K_V})p_V \gamma E ~ - ~ v_V V ~ + ~ A ~ \cdot ~ V ~ - ~ \mu ~ \cdot ~ V \\ \\ \frac{dV_c}{dt} ~ & = ~ p_{ihr} p_U(1 ~ - ~ p_{K_U})p_{K_V} p_V \gamma E ~ - ~ v_V V_c ~ + ~ A ~ \cdot ~ V_c ~ - ~ \mu ~ \cdot ~ V_c \\ \\ \\ P ~ & = ~ (S ~ + ~ E ~ + ~ I ~ + ~ R ~ + ~ H ~ + ~ H_c ~ + ~ U ~ + ~ U_c ~ + ~ V ~ + ~ V_c) \\ \\ \\ s ~ & = ~ 1 ~ + ~ a ~ cos \left (2\pi \frac{ \left (t ~ - ~ \left (\frac{365.25\phi}{12} \right) \right ) ~ + ~ t_{in}}{365.25} \right) \\ \\ \\ W ~ & = ~ W_{home} ~ + ~ W_{work} ~ + ~ W_{school} ~ + ~ W_{other} \\ \\ \\ \Lambda ~ & = ~ p ~ s ~ W ~ \cdot ~ \left (\frac{\rho E ~ + ~ I ~ + ~ C ~ + ~ \rho_s ~ \times ~ (H ~ + ~ H_c ~ + ~ U ~ + ~ U_c ~ + ~ V ~ + ~ V_c)}{P} \right ) \\ \\ \\ A ~ & = ~ \begin{pmatrix} \begin{pmatrix} -1 & 0 \\ 1 & -1 \end{pmatrix} & \ldots & 0 \\ \vdots & \ddots \begin{pmatrix} -1 & 0 \\ 1 & -1 \end{pmatrix} \ddots & \vdots \\ 0 & \ldots & \begin{pmatrix} -1 & 0 \\ 1 & 0 \end{pmatrix} \end{pmatrix} \\ \\ \\ p_{K_H} ~ & = ~ \begin{Bmatrix} 0 ~ \text{for} ~ H < K_H \\ 1 ~ \text{for} ~ H \geq K_H \\ \end{Bmatrix} \\ \\ p_{K_U} ~ & = ~ \begin{Bmatrix} 0 ~ \text{for} ~ U < K_U \\ 1 ~ \text{for} ~ U \geq K_U \\ \end{Bmatrix} \\ \\ p_{K_V} ~ & = ~ \begin{Bmatrix} 0 ~ \text{for} ~ V < K_V \\ 1 ~ \text{for} ~ V \geq K_V \\ \end{Bmatrix} \\ \\ \\ & \text{where model variables are defined as:} \\ \\ \\ S ~ & = ~ \text{Susceptible} \\ \\ E ~ & = ~ \text{Infected and incubating} \\ \\ I ~ & = ~ \text{Infected and asymptomatic following incubation} \\ \\ C ~ & = ~ \text{Infected and mildly symptomatic following incubation} \\ \\ R ~ & = ~ \text{Recovered and immune} \\ \\ H ~ & = ~ \text{Severe infection: hospitalised} \\ \\ H_c ~ & = ~ \text{Severe infection: not hospitalised due to lack of capacity} \\ \\ U ~ & = ~ \text{Severe infection: hospitalised in ICU} \\ \\ U_c ~ & = ~ \text{Severe infection: hospitalised and requiring ICU but placed in surge ward} \\ \\ V ~ & = ~ \text{Severe infection: hospitalised in ICU and on a ventilator} \\ \\ V_c ~ & = ~ \text{Severe infection: hospitalised in ICU requiring a ventilator but not on one} \\ \\ \\ & \text{and model parameters are defined as:} \\ \\ \\ W_{home} ~ & = ~ \begin{aligned} & \text{Country-specific age-dependent contact matrix describing the} \\ & \text{number of potentially infectious contacts at home per person per day} \end{aligned} \\ \\ W_{work} ~ & = ~ \begin{aligned} & \text{Country-specific age-dependent contact matrix describing the} \\ & \text{number of potentially infectious contacts at work per person per day} \end{aligned} \\ \\ W_{school} ~ & = ~ \begin{aligned} & \text{Country-specific age-dependent contact matrix describing the} \\ & \text{number of potentially infectious contacts at work per person per day} \end{aligned} \\ \\ W_{other} ~ & = ~ \begin{aligned} & \text{Country-specific age-dependent contact matrix describing the} \\ & \text{number of potentially infectious societal contacts per person per day} \end{aligned} \\ \\ \mu ~ & = ~ \frac{1}{\text{Age-dependent non-covid related death rate}} \\ \\ b ~ & = ~ \frac{1}{\text{Age-dependent fertility rate}} \\ \\ \alpha ~ & = ~ \frac{1}{\text{Duration in each category}} \\ \\ p ~ & = ~ \text{Probability of infection given a single contact} \\ \\ \gamma ~ & = ~ \frac{1}{\text{Duration of incubation period}} \\ \\ \rho ~ & = ~ \text{Relative infectiousness of incubating phase per contact} \\ \\ p_{clin} ~ & = ~ \text{Proportion of all infections that ever develop symptoms} \\ \\ \nu_I ~ & = ~ \frac{1}{\text{Duration of infectious phase}} \\ \\ \rho_s ~ & = ~ \text{Relative number of contacts for hospitalised patients} \\ \\ \omega ~ & = ~ \frac{1}{\text{Duration of immunity}} \\ \\ \alpha ~ & = ~ \text{Relative variation in transmissibility throughout the year} \pm \text{a proportion} \\ \\ \phi ~ & = ~ \text{Month of peak in transmissibility} \\ \\ t_{in} ~ & = ~ \text{Start date} \\ \\ p_{ihr} ~ & = ~ \text{Probability of an infection being severe (requiring hospitalisation) by age} \\ \\ p_{ifr} ~ & = ~ \text{Probability of an infection being fatal by age} \\ \\ \nu_H ~ & = ~ \text{Duration of hospitalised infection} \\ \\ \nu_U ~ & = ~ \text{Duration of ICU infection} \\ \\ \nu_V ~ & = ~ \text{Duration of ventilated infection} \\ \\ \delta_H ~ & = ~ \text{Probability of death for a hospitalised infection} \\ \\ \delta_{H_c} ~ & = ~ \text{Probability of death for an infection requiring hospital not get} \\ \\ \delta_U ~ & = ~ \text{Maximum death probability for a hospitalized infection requiring ICU admission} \\ \\ \delta_{U_c} ~ & = ~ \begin{aligned} & \text{Maximum death probability for a hospitalized infection that} \\ & \text{would require ICU admission but was not admitted to the ICU} \end{aligned} \\ \\ \delta_V ~ & = ~ \text{Maximum death probability for a hospitalized infection requiring a ventilator} \\ \\ \delta_{V_c} ~ & = ~ \begin{aligned} & \text{Maximum death probability for a hospitalized infection that} \\ & \text{would require a ventilator but did not get one} \end{aligned} \\ \\ p_U ~ & = ~ \text{Probability of an infected patient needing ICU} \\ \\ p_V ~ & = ~ \text{Probability of an infected patient needing ICU and a ventilator} \\ \\ p_{K_H} ~ & = ~ \text{Decision to assign a patient a hospital bed depending on capacity} \\ \\ p_{K_U} ~ & = ~ \text{Decision to assign a patient an ICU bed depending on capacity} \\ \\ p_{K_V} ~ & = ~ \text{Decision to assign a patient a ventilator depending on capacity} \end{aligned} \]
UN Department of Economic and Social Affairs Population Dynamics. Available from: https://population.un.org/wpp/Download/Standard/Population/.↩︎
European Centre for Disease Prevention and Control. Available from: https://www.ecdc.europa.eu/en.↩︎